Introduction
Earlier this week, I came across this X post on Monolith, Bytedance’s recommendation system. This system is used in BytePlus (Bytedance’s B2B SaaS wing) as well as TikTok. For an engineer interested in systems, this was an incredible paper that anyone with a basic background in CS could understand.
As I read through the paper, I knew I had to write about it for a couple of reasons:
- Much of the AI discourse currently surrounds LLMs, the models that power ChatGPT and Claude. While LLMs are certainly a powerful class of AI models, that’s not the entirety of machine learning. There are other paradigms out there that can teach us valuable lessons when building our own models and machine learning systems.
- Many of us know that TikTok’s recommendation algorithm is incredible, probably industry-leading. Why? It’s partially because of the architecture that they have built up. If we want to understand what makes the algorithm so good, it pays dividends to understand the engineering behind it
- Selfishly, I wanted to test my own writing skills to simplify Bytedance’s complicated engineering into something anyone could understand, even someone without CS knowledge.
This post will be describing the system that Bytedance employs, NOT the underlying model. I don’t think Bytedance will ever reveal how they constructed their recommendation model as that is their golden goose.
What is a recommendation system
Throughout this blog post, I am going to use the Netflix recommendation system as an example. Let’s recap the basic problem:
Millions of users are coming onto your platform and want to watch movies. However, you want to make sure that users are watching movies that they like. Why? That incentivizes them to stay on the platform, thus making you more money.
All recommendation systems, whether it be Amazon product recommendations or Instagram Reels, are variants of this problem.
As a Netflix engineer, the first thing you would want to do before you start getting into the system is to understand the inputs and the outputs. The input for these systems is a bunch of data on users and movies. User data may include their birthday, their location, the type of genres they have watched before, the last time they logged onto Netflix and more. Movie data might include the genre of the movie, the actors, the language, the length and more. How exactly would you represent this data? Most non-CS majors would immediately think of a spreadsheet! That’s usually right for basic recommendation systems.

In many modern systems, we can convert users, videos, and other items with lots of data into embedding vectors. To give a brief primer, a vector is a list of numbers. These embedding vectors have an overarching principle: similar items should have similar vectors. For example, if you and your best friend live in the same area and love the same movies, the embedding vector that represents you and your friend should be really similar! To convert all this data into a list of numbers for every single user and every single movie, we use something called embedding models. I am not going to go through the intricacies of embedding models, but feel free to jump to the resources section. The key thing to remember is that you are simply a list of numbers to the model. Nothing more, nothing less. To store these embeddings, we use embedding tables. This is simply a dictionary for embeddings that computers use to lookup your particular embedding when it wants to update its recommendation model.
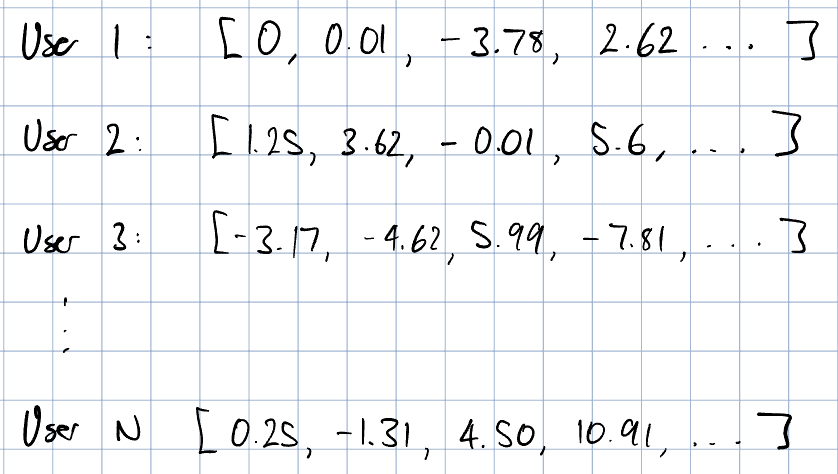
Our output for this problem is simple. Given a particular movie and a particular user and any other data, we want to determine the probability that the user would watch the movie. To do this, we need to train a recommendation model. A recommendation model is simply a program that takes in a bunch of parameters, including user and movie embeddings to produce this probability. For the sake of blog post scope, I am not going to describe the intricacies of recommendation models; I have linked some in the resources section.
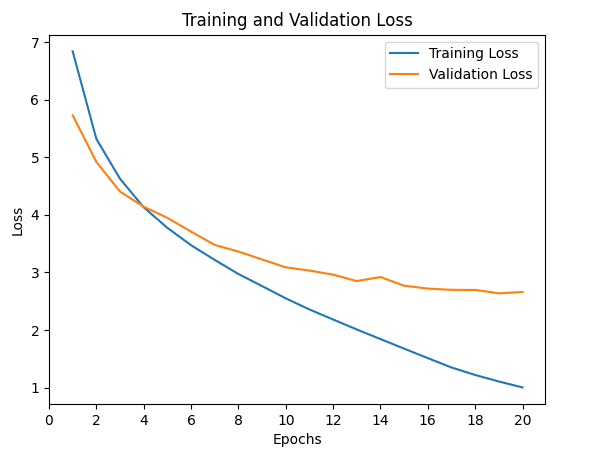
How do you actually train this model? The model starts off with a bunch of random parameters. It then takes an example of a user and associated features and then gives a prediction on whether the user will watch a particular movie. The model then compares the guess with what actually happened and then adjusts its parameters by a small amount so that it is more likely to get the correct answer next time. We do this over millions of examples, over and over again until our model performs well. We can track the error of our model across these examples in a loss curve as you can see below:
Problems with a naive recommendation system
From the above, you now have some basic principles that you can use to construct a basic recommendation system. However, things start to break down at scale. Let’s dive in.
Sparsity and dynamism
One big problem with large platforms is that there millions of users and millions of items. In the Netflix example, we want to encode every single movie and TV show into an embedding, that will take an insane amount of memory.
Another problem complicating is that interactions are long-tailed, i.e. there are a lot of movies that are interacted with extremely rarely. For example, there maybe a couple of Swahili-language movies that are interacted with relatively rarely compared to Hollywood rom-com TV shows. This leads to a problem of model training: how can a model learn to predict interactions accurately for the long-tail? It just doesn’t have that many examples to look at. A good way to conceptualize this is to hearken back to your math test days. Most of us learned how to solve the most common types of problems because that is what is most likely going to be asked on a test. However, many of us would struggle if the teacher threw a problem that we did not see before. This problem is known as sparsity.
The other major problem is dynamism. Let’s say that you were an engineer at Netflix in the early days and you were responsible for building out the first version of the recommendation system. You would train with users and movies and things would be swell for the first few months. However, when Netflix blows up, and are no longer constant; they are changing all the time. This makes it difficult to train a model since the input dimensions keep changing! However, we can mostly solve for this problem using a hash table, which allows us to add more rows dynamically as more movies/users are added to the platform.
Aside: what is a hash table?
Let’s step to a different example. You are a librarian and you have a million books. What is an easy way of organizing the books based on their title so you retrieve it easily?
Most people’s first answer is to organize alphabetically. When someone comes into your library looking for a book, you can search alphabetically like how you would in a dictionary. But can we do better than this? Yes! Let’s introduce the concept of a hash table.
A hash table is entirely based on hash functions, which takes an input and converts it in to a number. For example, if is the title of a book, a simple hash function could be: where the function just takes a remainder. For example, for the title “Harry Potter and the Prisoner of Azkaban”, would yield 40, which is the hash of the book. Now, we can associate the hash of a book title with its location in some sort of table. Now, all you need to do when someone looks for a book is to compute the hash and look at the associated location in the table. For computers, this is a far faster retrieval mechanism than searching through a sorted list.
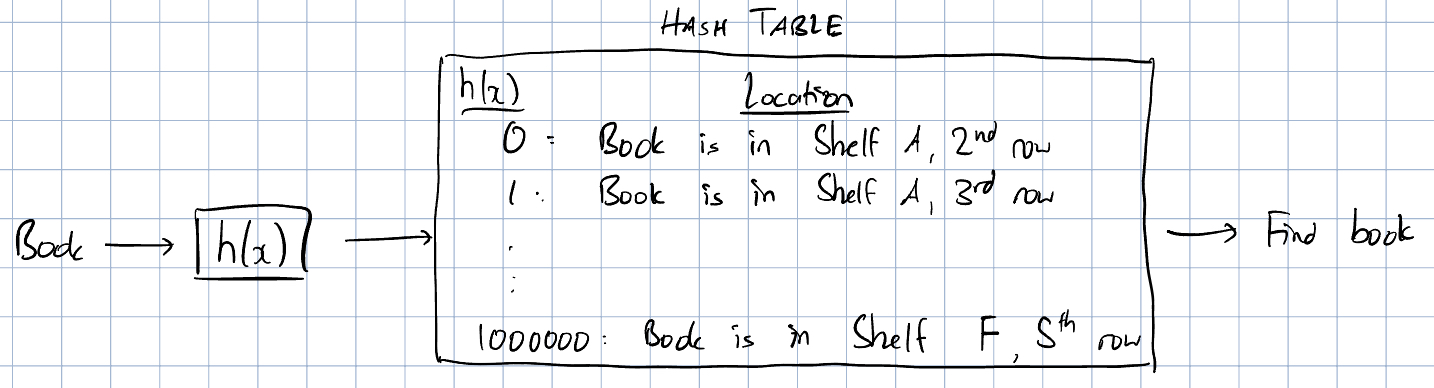
Let’s scale up the library problem. What if your library becomes extremely popular and you now have 2 million books? Well, if we use our same hash function, we’re going to run into some problems. For example, “The Girl with the Dragon Tattoo” actually works out to the same hash function output of 40. Now we have a dilemma: we have two books that have the same hashes. This will cause a conflict in our table as we now have multiple rows with the same hash, destroying the purpose of having a table in the first place. This action of multiple items hashing to the same output is known as collisions.
This is a problem with recommendation systems that use embedding tables at scale. It is almost a mathematical certainty that as more movies are produced and we keep hashing those movies using the same hash function that we will get collisions. How do recommendation systems solve this? They don’t! Many systems think that one embedding collision is not going to impact the model in any way, so might as well throw out the conflicting embedding or just ignore the collision.
But now we get to the real problem of hash tables with collisions. Let’s say that the hash of Interstellar clashes with the hash of a Czech-language movie. Under the previous assumption, we might just disregard Interstellar’s embedding and overwrite it with the Czech-language movie embedding, even though Interstellar’s embedding is used far more as more people are watching Interstellar. We just threw out good data! Furthermore, whenever our model runs into an interaction between a user and a Czech-language or an Interstellar movie, the same embedding will be used for training since the movies hash to the same embedding entry in the table. This embedding is going to be trained really poorly! A good analogy is if our brain used the same neural pathways to determine how to solve a calculus problem with how to kick a soccer ball; we will get confused.
Non-stationary distribution
Another problem with recommendation systems is that people change. You may not want to get Naruto Shippuden based rankings when you are 27 and you might want something more tasteful like Attack on Titan. This means that the probability distribution of a user watching a particular movie is non-stationary. For anyone who has taken statistics, you will immediately know that non-stationary data is extremely annoying to model.
For engineers, this means that we need to change our model whenever viewer trends change. We can’t just train it once and call it a day. For apps like TikTok, we need to train these models in near real-time as trends can come and go within a matter of days. This requires us to build a system that is capable of both batch (huge amount of data) and online (real-time, incremental data) training of models.
How does Bytedance solve these problems?
A new type of hash table
We first want to solve the issue of sparsity and dynamism. Bytedance decided to use a souped-up version of cuckoo hashing.
Cuckoo hashing is really simple. Rather than having one table with one hash function, we now have 2 tables, one with hash function and another with hash function . When we add an item to the cuckoo hash table, we park it in table 1 using hash function . If we find that the table row is already occupied, we kick out the item in table 1 and replace it with the new item. We then go to table 2 and hash the kicked out item using and see if we can find an empty spot. If we do, we are done. If not, we kick out whatever is occuping table 2 and hash to table 1. We keep doing this until everything settles down. Now, if we want to find an item, we use both and and see if the item exists in either table. Mathematically, we can prove that cuckoo hashing will theoretically never have collisions.
Aside: why is it called cuckoo hashing? Although cuckoo birds seem innocent, they are monsters who do this exact same thing as a kid. Cuckoos lay their eggs in other bird species’ nests and the baby cuckoo bird will kick out the other birds. Cute appearances belie horrible behavior.
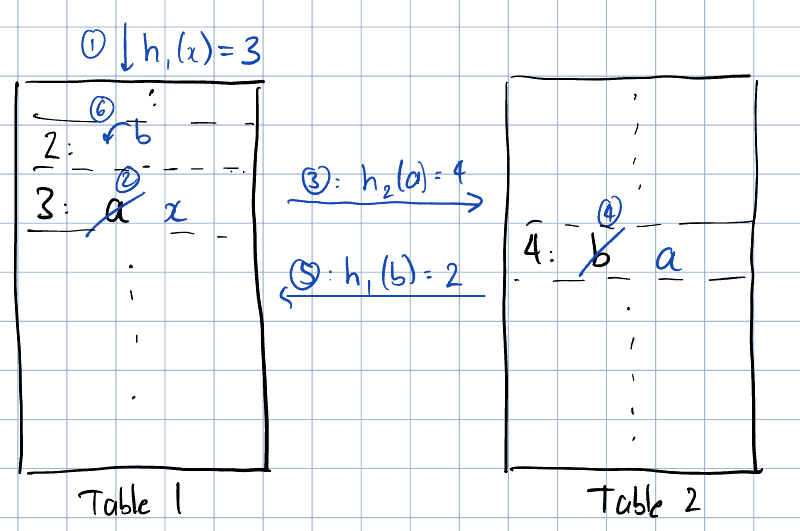
Cool, so we have a new hash table with this no-collision property. There’s still a problem. In TikTok, millions of videos are being created EACH DAY. If we keep hashing videos and storing their embedding using this hash table, we are going to kick out some videos from the table as our table cannot be infinitely large and we can’t keep hashing videos again and again. Bytedance looked at their data to see how they can constrain the size of their table. They noticed a couple of things:
- Infrequent items/users are not very helpful for models: The weird Alibaba Express light up samurai swords that are not seen that often are not going to meaningfully improve model performance. Does the embedding of this video really need to be stored if its going to be useless?
- Old items/users are not very helpful for models: The user that has not logged on in months and the “Damn Daniel” videos are not very helpful. Again, do we need to store their embeddings if they aren’t useful?
Given these insights, Bytedance added filters to videos & users before they are added to an embedding table: they must pass some sort of frequency threshold (eg. users must log in number of times, videos must have views). Also, they set up their embedding tables to kick out old embeddings every days.
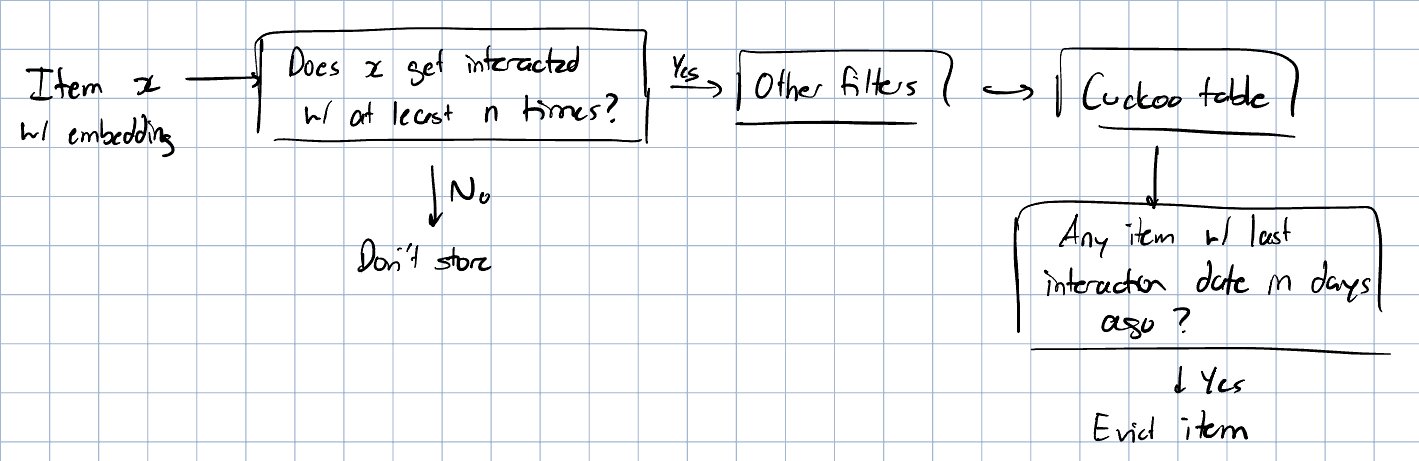
With this, the embedding table is now a lot smaller and can be used more effectively for model performance and training.
An ingenious system of near real-time training
To train models, TikTok uses the Worker-ParameterServer (PS) architecture of TensorFlow, which is extremely simple. You have one master computer that splits different parts of model training across worker and parameter server pairs. The worker computer does the model computations, while the parameter server stores the parameters that the worker needs to train its part of the model. If you have multiple worker-PS pairs, you can effectively parallelize model training.
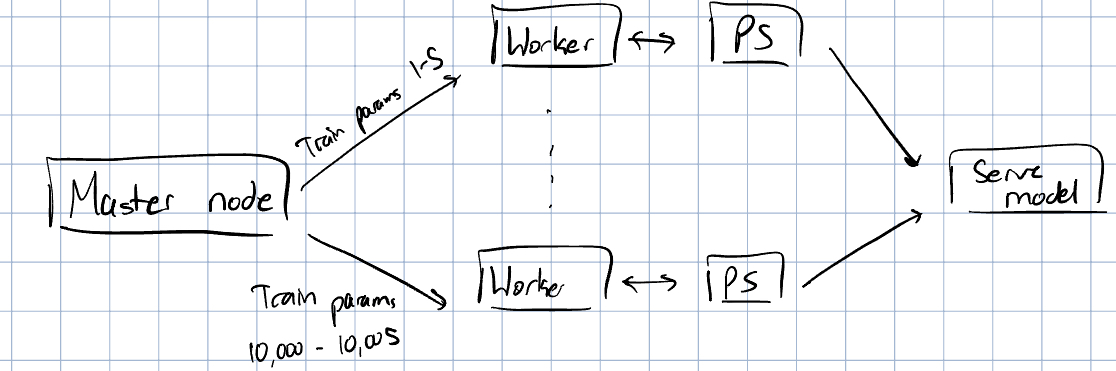
To train a whole new model, you would need to do batch training, where you take millions of data rows to train the model across all these worker-PS pairs which could take several days. However, if you just want to update a model based off a few user-movie interactions, you don’t need to do all that work. You really only need to update the embeddings of the user and the movie that they watched and this should only take a few minutes (online training). This leads us to a question: can you create an architecture that can support both batch and online training?
Monolith
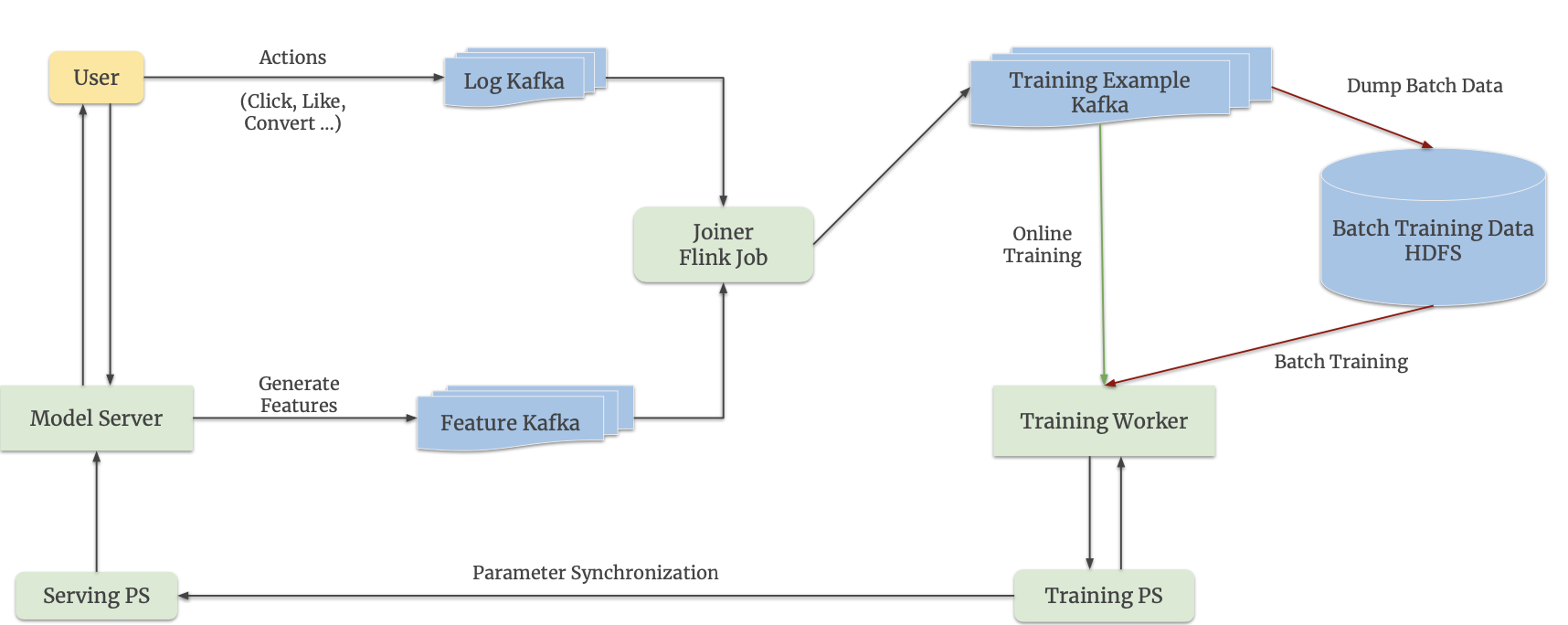 This is the system design architecture of Monolith. Let’s go over this step by step through the example of Netflix (assuming Netflix is using this architecture).
This is the system design architecture of Monolith. Let’s go over this step by step through the example of Netflix (assuming Netflix is using this architecture).
The fist thing important note in this diagram is that there are actually two models: a serving model and a training model. The serving model is a highly-available model that all users will interact with and it is stored in the model server and serving PS. The second model is the one we are continuously training, which is stored in the training worker-PS pair.
Let’s say that I am a user that just started watching a new episode of Shogun and Netflix deems this an interaction worthy of updating the model. The first thing we are going to do is give the user its recommendations based off the serving model we already have. To actually train the model, we are going to keep track of the interaction and the associated embeddings (eg. my embedding as well as the embedding of Shogun).
Since there are millions of interactions every minute, we want to put this in queues (these specific queues are Kafka queues, not that important to this article) so we can process the interactions and embeddings one at a time. This gets passed into a joiner. The joiner has two responsibilities:
- Match the user interaction with the embeddings of the user & the movie
- Negative sampling: In reality, there are going to be far more negative interactions than positive ones. For example, a negative interaction could be me clicking into a show but not actually watching it. This happens way more often than me actually watching the show. To make sure our model is trained on equal amounts of both positive and negative interactions, we just take a sample of all the negative interactions rather than passing in everything to the model training section of the architecture.
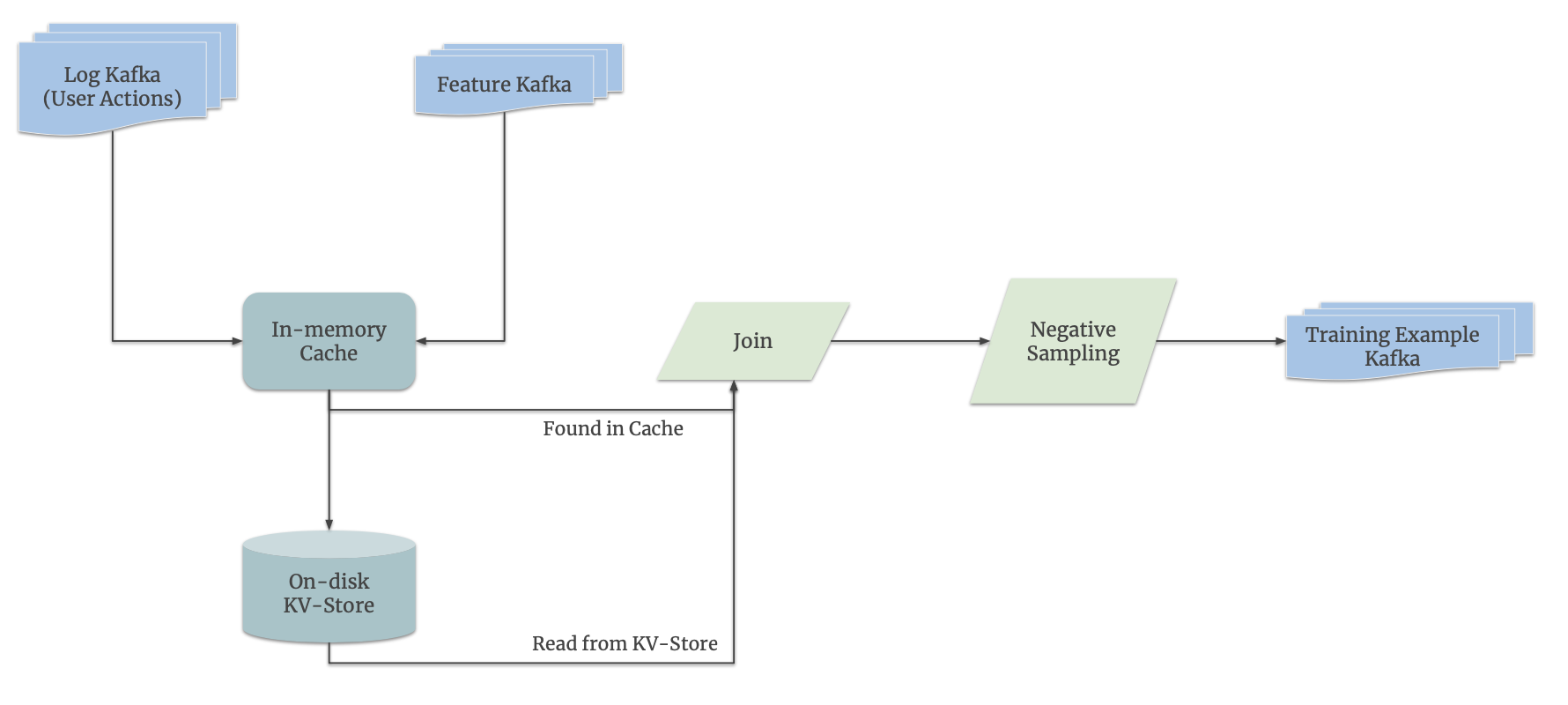
Once we have these features and interactions nicely joined, we will first dump it into a large database for future batch training purposes. For online training, we immediately send this example to the training worker-PS pair and ask it to adjust parameters/embeddings such that it would be more accurate in predicting the interaction the next time it comes up. These updated parameters gets stored in the training PS.
How do you update a live model?
We now have our model updated and ready to be deployed to users, but how exactly do you that? A naive solution is to just replace all the parameters in the model PS with the parameters in the training PS. There are a few problems with this solution:
- Removing all the parameters and replacing it will take the model offline. The masses could not tolerate this.
- This is a LOT of data to pass between the training server and the model server. Best case scenario, this will just be a slow process of updating. Worst case scenario, our network could suffer some serious consequences with all this data being sent.
Bytedance took a deeper look at the data and found the following insights:
- Sparse features dominate model size: Features that are irregularly interacted with (eg. user embeddings, video embeddings) are actually what dominate the model size. It’s not the model architecture parameters that is causing the problem
- Only a couple parameters are being updated: During online training on a couple of user interactions, only a few user and video embeddings are being updated. The other parameters in the model usually don’t change because those parameters are affected in every single training run, so a few examples will not meaningfully change it. A good example of this is when you are learning calculus. Every new problem you do updates your understanding on calculus but it won’t do much for your understanding of basic arithmetic, since you use basic arithmetic all the time.
Using these insights, Bytedance did the following:
- During model training, keep a list of embedding IDs that are updated
- Only update those embeddings in the model PS every minute
- Update dense parameters on a reduced frequency (eg. every week/month)
By doing this, Bytedance is able to continuously train and update its massive recommendation model without memory constraints or taking the model offline.
Takeaways
While this is some really interesting CS work and has meaningfully optimized Bytedance’s recommendation system, I don’t actually think Bytedance created any groundbreaking innovations here. Most CS students who have done a data structures course would immediately understand this approach.
Instead, the main takeaway from this paper is how Bytedance used their data effectively to create good heuristics. It is with those heuristics that they were able to cut down on embedding table sizes and update models in real-time. For any engineer reading this article, I hope you can take this same lesson away. There are lots of interesting technical solutions out there for a variety of problems, but often the answer lies in something far simpler. Take a look at your data and see what you can do with existing data patterns before you create an overcomplicated engineering system.